Home Page or Table of Contents
Dynamic range can be SINGLE-TONE or TWO-TONE.
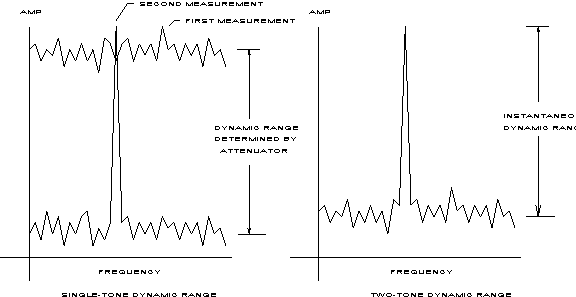
SINGLE-TONE refers to the ability of a device to measure the strength of CW tones by inputting them one at a time and using an adjustable attenuator to set the level such that the maximum signal level does not saturate the device for each measurement.
TWO-TONE refers to the ability of a device to measure the strength of two or more CW tones simultaneously. This is a far more stringent requirement that SINGLE-TONE dynamic range, since the attenuator adjustment is good for the strongest tone only.
A gain in SNR can be achieved by increasing the observation time of the CW signal. Because the signal power increases linearly with integration time, while the noise power increases by the square root, a net gain of 3 dB can be obtained by doubling the integration time (6 dB Signal gain minus 3 dB Noise gain = 3 dB gain in SNR). This gain is most easily viewed in the frequency domain, where the sample size can be increased from, say, 128 to 256, then to 512, 1024, etc., and the effect observed by noting the value of the spectral noise floor.
SNR AND A/D CONVERTERS An A/D converter will generally give a 6-dB increase in SNR for each additional bit of resolution. If, as mentioned above, the noise is assumed to be Gaussian in the LSB of the converter, integration gain will produce an additional 3 dB for each doubling of the input sample size. This is true, even if the input signal is much less than the LSB of the converter. For instance, a 12-bit A/D and a 1024-sample input size will produce a TWO-TONE dynamic range of approximately 6 x 12 plus 3 x 10 = 102 dB. This implies that a full-scale signal and a second signal over 100-dB down from the full-scale signal can be simultaneously observed. This is, in fact, the case. The mathematical details are given below.
and RMS NOISE=10 log10 (1/(12x2n-1))
where the A/D has k bits (12, for the above example), the sample size is n (1024, for the above example), and the noise is uniformly distributed over the interval [1/2,-1/2] (half the LSB of the A/D) such that its average power level (variance) is equal to 1/12. By doing the arithmetic, the approximate result may be written as:
which is equivalent to an increase in SNR of 6dB for each additional A/D converter bit and an increase in SNR of 3 dB for each doubling of the sample size.
AGC, or Automatic Gain Control, is often applied by using the overall noise power level to control an electronic attenuator. Note, however, that for two-tone dynamic range to be maximized, the AGC should be done such that the noise resides in the interval [1/2,-1/2] of the LSB.