Huffman Coding

Many computers use 8-bit bytes to represent the letters A through Z, the numbers 0-9, and various other symbols. The use of an 8-bit byte to represent a total of 256 separate ASCII symbols is an example of so-called "block" coding. In block coding, all code frames have the same length, regardless of the frequency with which any particular code frame occurs. Thus, for instance, the the ASCII symbols 'e' and 'z' are both represented by 8-bit code frames, even though in common usage the letter 'e' occurs far more often than the letter 'z'. In other words, block coding takes no advantage of the actual frequency of usage of the individual characters as a means of reducing the code frame size. During the execution of a program, block coding offers great advantages in terms of speed and simplicity in fetching and manipulating symbols. However, for purposes of storage and transmission other schemes offer significant advantages.

When Morse and Vail constructed the telegraph code, they sought to minimize the time and effort required to transmit ordinary message traffic, and in doing so intentionally avoided the use of block coding. Instead, they undertook to empirically determine the relative frequency of occurrence of alphabetic symbols in written text. Thus, in Morse code the letter 'e' is represented by a code frame of length 1 (a single dot), whereas the letter 'z' is represented by a code frame of length 4 (dash-dash-dot-dot).

Unblocked codes, such as Morse code, are sometimes referred to as "compressed" codes, because they shorten or "compress" the amount of time or space required to transmit and/or store a given amount of information. An excellent example of how data compression can be performed in a systematic manner is demonstrated by Huffman codes. Huffman codes are quite easy to generate, and an overview of their characteristics and how to mechanize them is given below:

OBJECTIVE

Store/transmit a maximum amount of information in a minimum amount of space/time.

APPROACH

NON-BLOCK -- make code words as short as possible by assigning the shortest code words to those symbols with the highest probability (frequency of occurence)
NON-SINGULAR -- Each code symbol should be distinct from all other code symbols.
UNIQUELY DECODABLE -- No code symbol should be the prefix of another code symbol (known as the "prefix" property).
INSTANTANEOUS -- Decoding (data recovery) should be sequential with no dependence on the preceding symbol.
SYNCHRONIZATION -- The decoding may be started anywhere within the message, with synchronization occurring after only a few errors due to missed codes.
REDUNDANCY -- There should be minimal redundancy in the code.

Despite the fact that these requirements may seem formidable, they are easily met by Huffman codes. The method of generating such codes is straightforward and is illustrated below using a typical Huffman encoding scheme as applied to an imaginary set of data:

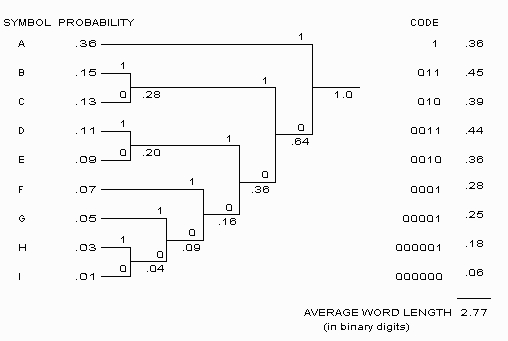
The encoding procedure consists of the following steps:

List the symbols along with their probabilities in a vertical column in descending order, with the highest probability at the top and the lowest probability at the bottom.
Connect each of the probabilities in a pair-wise fashion, always joining the lowest two unused probabilities until the probabilities merge to a single point (this process is called "binary fusion").
Assign 1's and 0's to each of the pairs throughout the horizontal tree. Assigning 0's and 1's can be done as shown, or with the 0's and 1's reversed, yielding a complementary code.
To obtain the code for each source symbol, trace the path from the symbol on the left to the final single point on the right, then read the sequence of 0's and 1's backwards through the tree from right to left.

The average word length shown on the right is calculated by multiplying the length of the code for a given symbol by the probability for that symbol and then summing these together for all codes. This length, when divided into the length of a hypothetical block code length which might be used if compression were not applied (such as the 8 bits in a single byte), represents the degree of compression which can be obtained. Obviously, the accuracy of this estimate is highly dependent on the degree to which a given data set matches the statistics used. For example, if this procedure were applied to the 26 characters of the alphabet and then used to transmit a sequence consisting of nothing but the letter 'z,' the resulting compression would be worse than if the original block code had been used. Similarly, using codes intended for compression of written information to compress other types of data will often yield very marginal results.

In order to tailor data sets in a manner which will result in efficient codes, use is frequently made of so-called "delta-modulation" techniques, which can act to decrease the statistical "entropy" of a given data set. Information on this process can be found under Minimum-Entropy Differencing.

Home Page or Table of Contents