Home Page or Table of Contents
Interpolation between sampled data points is often called for, either in the time or in the frequency domain. Thre are, in general, two useful techniques:
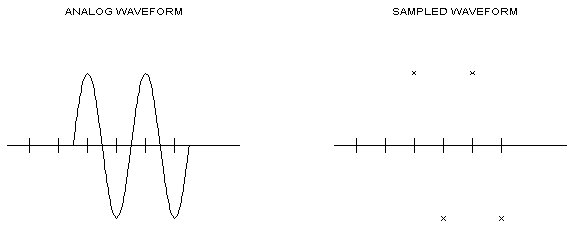
SINGLE-POINT INTERPOLATION -- For purposes of illustration, a baseband analog waveform consisting of a simple sine wave is sampled at exactly the Nyquist frequency, i.e., two samples are taken for each cycle:
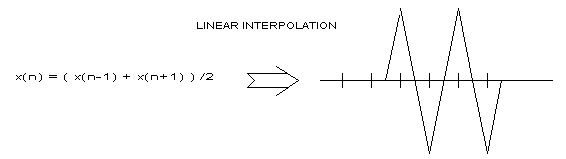
If such a waveform were to be processed using linear interpolation, the resulting waveform would look as follows:
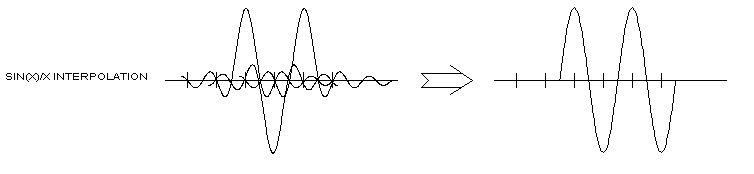
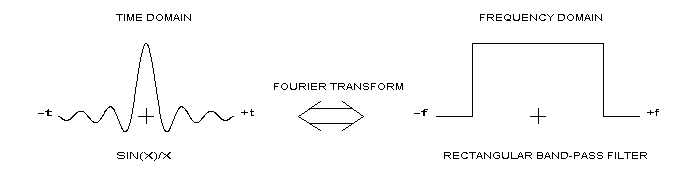
A more useful alternative is to convolve the waveform with the impulse response of the bandpass filter used to sample the waveform. If this filter is roughly rectangular, then the double-sided sin(x)/x approximation is appropriate:
The implementation is done as shown below:

A sin(x)/x waveform (sometimes called the "sinc" function) is centered at each sample point, with its successive left and right zeros intersecting the time axis at each of the other sample points. Interpolation is accomplished by adding up the contributions of all the sin(x)/x waveforms at the time point to be interpolated. The number of cycles of the sin(x)/x waveform to be used depends on the accuracy or precision desired (see Measurement (Accuracy vs. Precision) , which can be a function either of amplitude or of phase. A typical amplitude criterion is to require the amplitude error to be less than the LSB of the A/D convertor. A typical phase criterion (assuming both In-phase and Quadrature channels are present) is to require that the phase error be less than that of the hybrid device used to derive the I/Q separation. The interpolation procedure is applied to each of the I and Q channels separately. (The fact that the sinc function is infinite in extent and decays slowly is sometimes dealt with by using a taper on the sinc function.)
Interpolation in the frequency domain is identical to that in the time domain and is a function of the time-domain window used. If no time-domain window is used, then the implied window is rectangular and the frequency-domain waveform is, again, sin(x)/x.
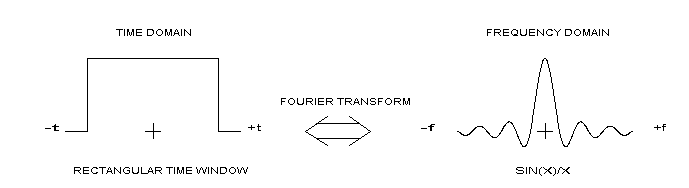
If a time-domain window is used, then the frequency-domain waveform should be modified accordingly. The frequency-domain usually involves interpolation in both the I and Q channels, since most frequency-domain data is in complex form (even pure-real data results in a complex Fourier transform, even though the negative frequencies are the complex conjugates of the corresponding positive frequencies).
In practice, for ease of implementation, it is not uncommon to use a sin(x)/x window as a reasonable approximation for either time-domain or frequency-domain data, since sin(x)/x can be evaluated analytically (without table lookup).
BLOCK OR ARRAY INTERPOLATION
Because convolution is a computationally tedious process, interpolation of an entire time-domain array is done more efficiently by transforming the data to the frequency domain, extending (padding) the frequency-domain data with zeros and inverse transforming back to the time domain. The zero-padding effectively extends the bandwidth, and thereby the sample frequency, effectively performing interpolation. (see Time and Frequency Resolution)
Similarly, interpolation of frequency-domain data can be accomplished by transforming the data to the time domain, extending (padding) the time-domain data with zeros and inverse transforming back to the frequency domain. The zero-padding effectively increases the time window, and thereby the frequency resolution, effectively performing interpolation. (see Time and Frequency Resolution)
The question sometimes arises as to how to handle the combination "d.c. + N/2" frequency point during zero-padding in the frequency domain. This point should not be moved to the end of the array during zero-padding, but simply left in place.